如何求解简单情况下的NS方程?《张朝阳的物理课》推导椭圆管中
如何求解简单情况下的NS方程?《张朝阳的物理课》推导椭圆管中
探索NS方程的秘密:《张朝阳的物理课》如何推导椭圆管中的流量公式
在物理学中,纳维-斯托克斯方程(Navier-Stokes Equations,简称NS方程)无疑是一个重要的里程碑。这组方程描述了粘性流体运动的基本规律,是流体力学中的核心理论之一。然而,NS方程的复杂性使得求解变得异常困难,即便是对于简单的情况,也需要借助先进的数学工具和计算技术。今天,我们将跟随《张朝阳的物理课》的脚步,探索如何求解简单情况下的NS方程,并特别关注椭圆管中粘性流体的流量公式推导。
一、NS方程的挑战与魅力
NS方程是一个非线性偏微分方程组,它涉及到多个变量和复杂的相互作用。这种复杂性使得求解NS方程成为一项极具挑战性的任务。然而,正是由于其强大的描述能力,NS方程在流体力学、气象学、航空航天工程等领域发挥着至关重要的作用。
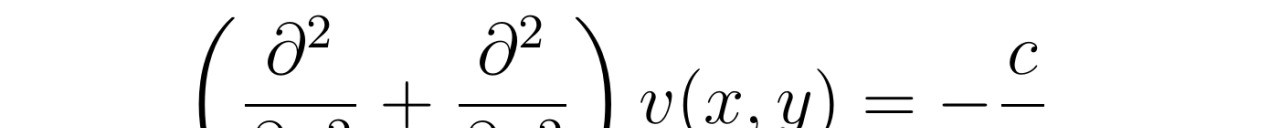
二、简单情况下的NS方程求解
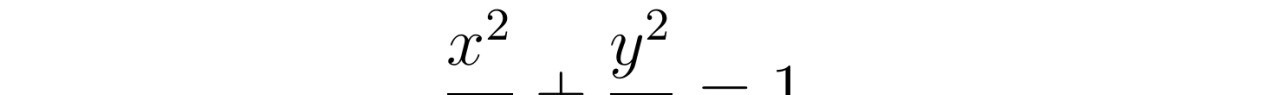
对于简单情况下的NS方程,我们可以采用一些简化和近似的方法来进行求解。例如,在无粘性流动的情况下,NS方程可以简化为欧拉方程,此时可以使用贝克隆公式等方法得到解析解。然而,在实际应用中,大多数流体都是具有粘性的,因此我们需要考虑粘性对流体运动的影响。
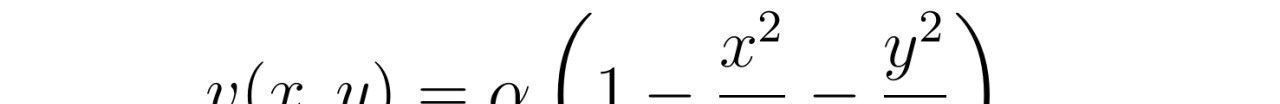
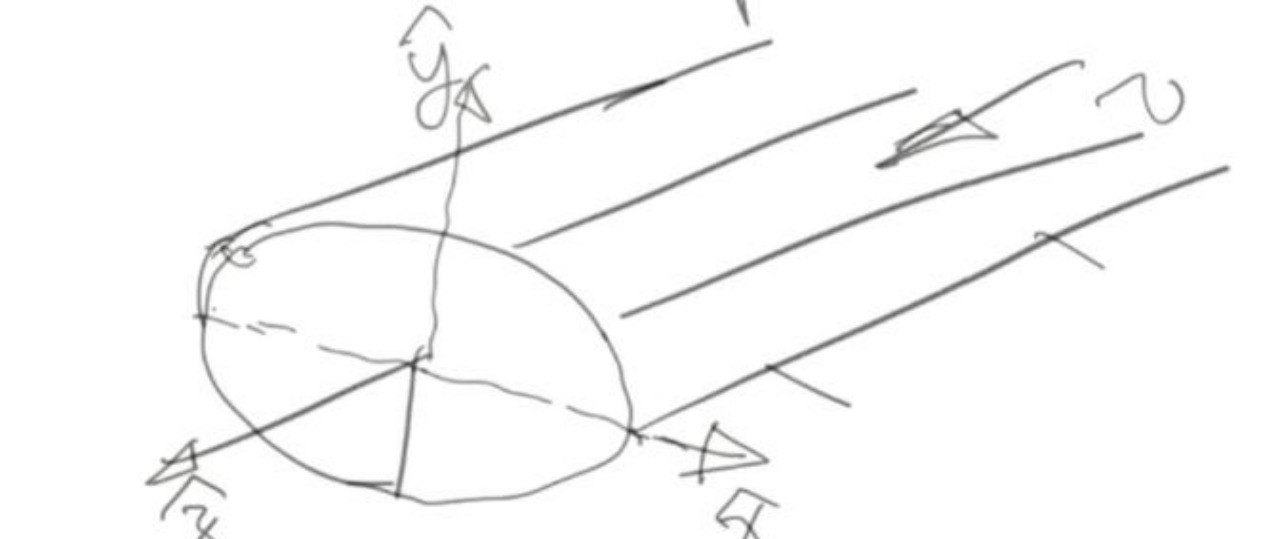
在《张朝阳的物理课》中,张朝阳教授通过引入椭圆管模型,展示了如何在特定情况下求解NS方程。椭圆管模型是一个理想化的物理模型,其横截面始终保持为椭圆形状。在这个模型中,我们可以建立直角坐标系,将z轴置于椭圆管的中心,xy平面切出一个椭圆截面。通过设定合适的边界条件和初始条件,我们可以将NS方程转化为一个可解的偏微分方程。
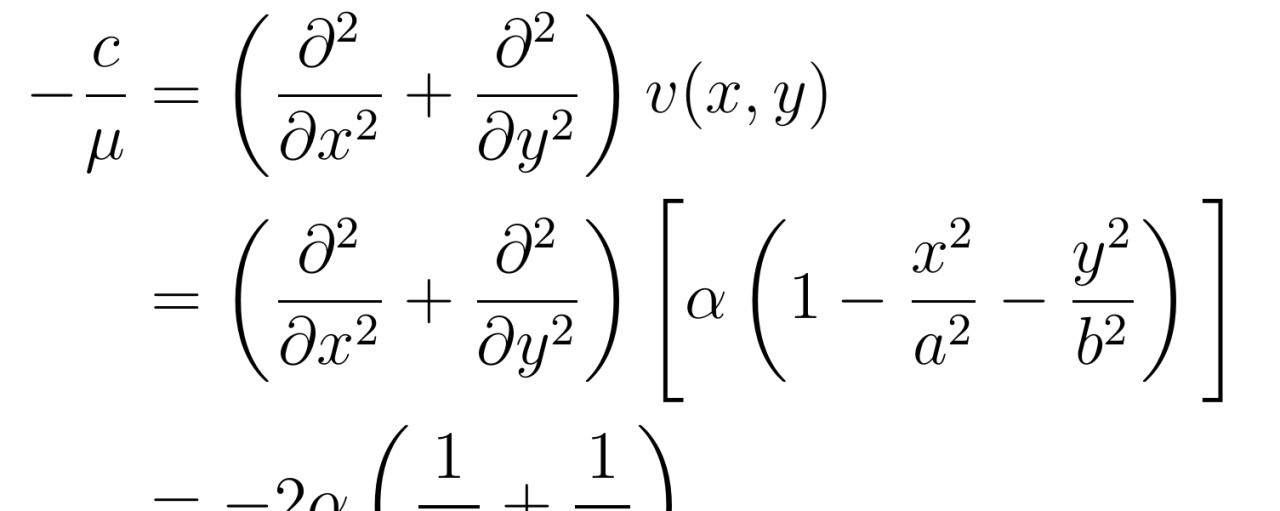
三、椭圆管中流量公式的推导
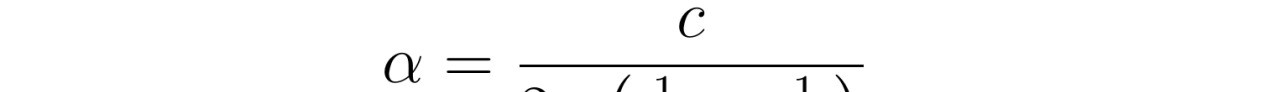
在椭圆管模型中,我们需要关注的是流体在管内的流量。流量是描述流体通过管道体积速率的重要参数,对于工程设计和实际应用具有重要意义。在《张朝阳的物理课》中,张朝阳教授利用NS方程和椭圆管的几何特性,推导出了椭圆管中粘性不可压缩流体的流量公式。
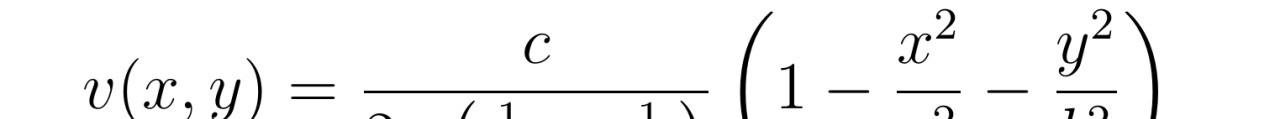
推导过程中,张教授首先建立了流体在椭圆管内的流速分布模型。根据泊肃叶流动的特点,流速在边界处恒为零,而在管道中心处达到最大值。通过设定流速的边界条件和初始条件,张教授将NS方程转化为一个可解的偏微分方程。然后,他利用数学方法和计算技术求解这个方程,得到了流速在椭圆管内的分布函数。

最后,张教授对流速分布函数进行积分运算,得到了椭圆管中粘性不可压缩流体的流量公式。这个公式不仅具有理论价值,还可以为工程设计和实际应用提供重要参考。
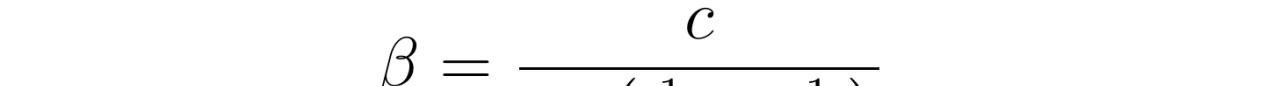
四、科技领域的新动态与未来发展趋势
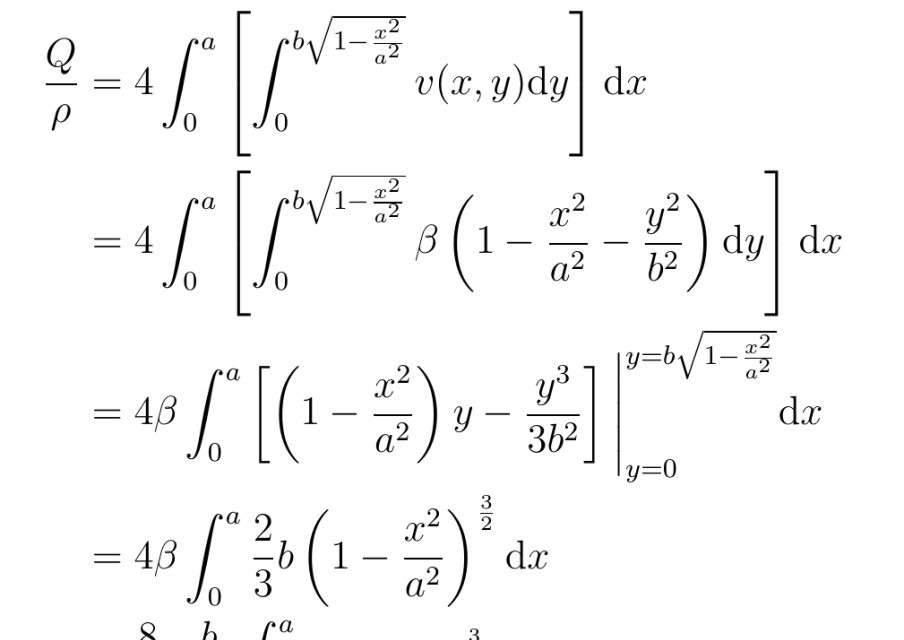
通过《张朝阳的物理课》对NS方程和椭圆管流量公式的探讨,我们可以看到科技领域在理论研究和实际应用方面的不断进步。随着计算技术的飞速发展,我们已经能够处理更加复杂和精细的物理模型,从而得到更加准确和可靠的结果。
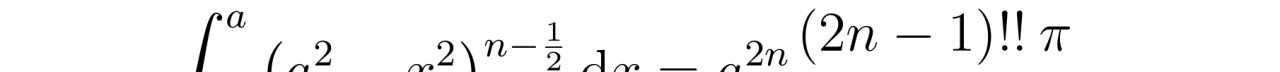
未来,随着人工智能、大数据等技术的不断成熟和应用,我们有理由相信科技领域将会迎来更加广阔的发展空间和更加美好的未来。在这个过程中,我们也需要不断学习和探索新的知识和技术,以应对不断变化的挑战和需求。
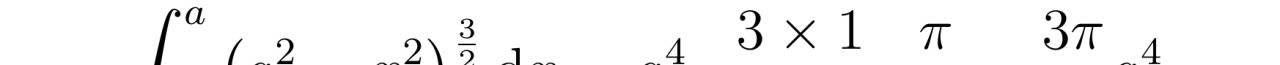
总结而言,《张朝阳的物理课》为我们提供了一个深入了解NS方程和椭圆管流量公式的机会。通过学习和掌握这些知识和技术,我们可以更好地理解流体运动的规律和特性,为工程设计和实际应用提供有力支持。同时,我们也需要关注科技领域的新动态和未来发展趋势,以便更好地适应和应对不断变化的挑战和需求。
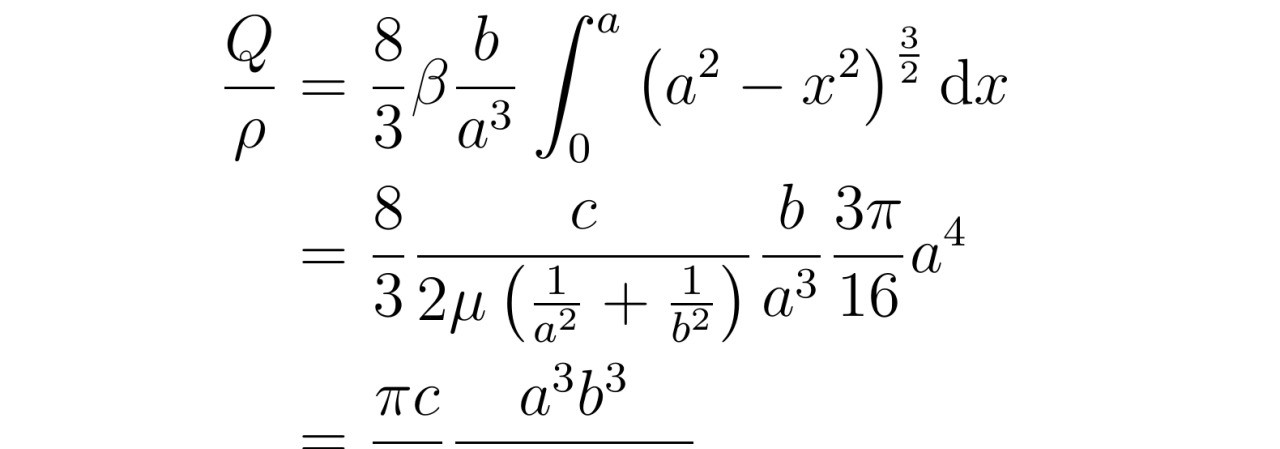
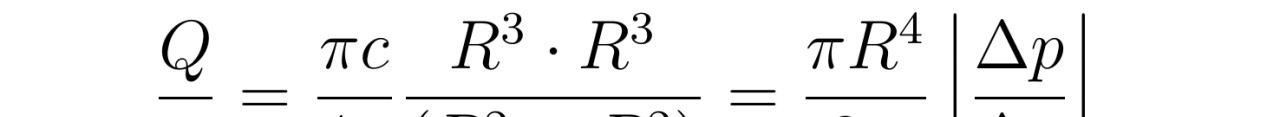

-

- 欺诈的定义和例子
-
2025-12-28 13:06:24
-

- 永不消失的电波
-
2025-12-28 13:04:09
-

- 全国47所高中排名!第一名居然是河北衡水高中,清华附中排第三?
-
2025-12-28 13:01:55
-

- 韩国国民咖啡——MAXIM的前世今生
-
2025-12-28 12:59:41
-

- 蹦床公主何雯娜,为何放弃吊环王陈一冰,转身嫁给长相普通的梁超
-
2025-12-28 12:57:26
-

- 他是最年轻的开国少将,官至大军区副司令员,69岁因车祸去世
-
2025-12-28 12:55:12
-

- 精选适合冬季游玩的城市
-
2025-12-27 05:53:06
-
- 泗阳:城市有温情 百姓更幸福
-
2025-12-27 05:50:51
-
- 分享全国县级城市:黑龙江(12)——泰来县
-
2025-12-27 05:48:37
-

- 中国最著名的5条步行街,分别在这五个城市
-
2025-12-27 05:46:23
-

- 东北曾经辉煌过的城市有哪些?
-
2025-12-27 05:44:09
-

- 【创建文明城市】巴林左旗教育系统:多措并举扎实推进创建自治区文明城市工作
-
2025-12-27 05:41:54
-
- 2020年2月南加州大洛杉矶主要城市房产交易报告
-
2025-12-27 05:39:40
-

- 天津:从二线城市走向一线?
-
2025-12-27 05:37:26
-
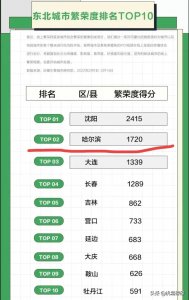
- 东北城市繁荣度排名出炉,沈阳与哈尔滨大幅领先大连、长春等城市
-
2025-12-27 05:35:11
-

- 湖南最小的城市湘潭市别名“莲城”“潭城”
-
2025-12-27 05:32:57
-
- 最新!2019上半年中国城市GDP百强榜单
-
2025-12-26 15:35:41
-

- 小本创业无需门面,4个小城市稀缺项目,穷人翻身的不二出路!
-
2025-12-26 15:33:27
-

- 中国宜居城市最新排行榜!第一名曾霸榜七年!
-
2025-12-25 22:56:19
-

- @淮北人 这些全国文明城市知识,get起来!(上)
-
2025-12-25 22:54:05



 五本评分很高的自闭症男主文:你拥有全世界,而我的世界只有你
五本评分很高的自闭症男主文:你拥有全世界,而我的世界只有你 1995年,吴毅将与钟淑慧合作限制级电影,尺度敏感删减9分钟
1995年,吴毅将与钟淑慧合作限制级电影,尺度敏感删减9分钟 每日推书!五本牧场流小说,平平淡淡,我就养牛养马
每日推书!五本牧场流小说,平平淡淡,我就养牛养马 宝藏女孩——陈钰琪全图写真合集
宝藏女孩——陈钰琪全图写真合集 解放战争,林彪为何被叫“101”?这个代号有何寓意?
解放战争,林彪为何被叫“101”?这个代号有何寓意? 史上最全QQ官方经典头像全面翻新,不光高清还会动
史上最全QQ官方经典头像全面翻新,不光高清还会动 潘春春:从陕北放羊娃到“中国波霸”的逆袭人生
潘春春:从陕北放羊娃到“中国波霸”的逆袭人生 推荐九本模拟经营小说,经营领地和商铺(二)
推荐九本模拟经营小说,经营领地和商铺(二) 圣女贞德:美貌绝伦,率军抗击侵略者,落入敌手惨遭凌辱受刑而亡
圣女贞德:美貌绝伦,率军抗击侵略者,落入敌手惨遭凌辱受刑而亡 《温柔的谎言》女主安然的堕落,到底是因为爱慕虚荣还是被陷害?
《温柔的谎言》女主安然的堕落,到底是因为爱慕虚荣还是被陷害?